რისთვის გამოიყენება ეპიციკლური გადაცემათა კოლოფები?

ეპიციკლური მექანიზმებიასევე ცნობილია, როგორც პლანეტარული გადაცემათა სისტემები, ფართოდ გამოიყენება სხვადასხვა ინდუსტრიაში მათი კომპაქტური დიზაინის, მაღალი ეფექტურობისა და მრავალმხრივი გამოყენების გამო.

ეს მექანიზმები ძირითადად გამოიყენება იმ ადგილებში, სადაც სივრცე შეზღუდულია, მაგრამ მაღალი ბრუნვის მომენტი და სიჩქარის ცვალებადობა აუცილებელია.

1. საავტომობილო ტრანსმისიები: ეპიციკლური გადაცემათა კოლოფი ავტომატური ტრანსმისიების ძირითადი კომპონენტია, რომელიც უზრუნველყოფს გადაცემათა შეუფერხებელ გადართვას, მაღალ ბრუნვის მომენტს დაბალი სიჩქარით და ეფექტურ სიმძლავრის გადაცემას.
2. სამრეწველო დანადგარები: ისინი გამოიყენება მძიმე დანადგარებში მაღალი დატვირთვების მართვის, ბრუნვის მომენტის თანაბრად განაწილებისა და კომპაქტურ სივრცეებში ეფექტურად მუშაობის უნარის გამო.
3. აერონავტიკა: ეს მექანიზმები გადამწყვეტ როლს ასრულებს თვითმფრინავის ძრავებსა და ვერტმფრენის როტორებში, რაც უზრუნველყოფს საიმედოობას და მოძრაობის ზუსტ კონტროლს რთულ პირობებში.
4. რობოტიკა და ავტომატიზაცია: რობოტიკაში ეპიციკლური მექანიზმები გამოიყენება მოძრაობის ზუსტი კონტროლის, კომპაქტური დიზაინისა და შეზღუდულ სივრცეებში მაღალი ბრუნვის მომენტის მისაღწევად.

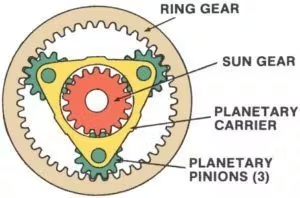
რა არის ეპიციკლური გადაცემათა ნაკრების ოთხი ელემენტი?

ეპიციკლური გადაცემათა ნაკრები, ასევე ცნობილი როგორცპლანეტარული მექანიზმი სისტემა წარმოადგენს მაღალეფექტურ და კომპაქტურ მექანიზმს, რომელიც ხშირად გამოიყენება საავტომობილო ტრანსმისიებში, რობოტიკასა და სამრეწველო დანადგარებში. ეს სისტემა შედგება ოთხი ძირითადი ელემენტისგან:

1. Sun Gearგადაცემათა ნაკრების ცენტრში განთავსებული მზის გადაცემათა კოლოფი მოძრაობის მთავარი მამოძრავებელი ან მიმღებია. ის პირდაპირ კავშირშია პლანეტარულ გადაცემათა კოლოფებთან და ხშირად სისტემის შემავალ ან გამოსავალ სიგნალს წარმოადგენს.

2. პლანეტა გეარსიეს არის მრავალი გადაცემათა კოლოფი, რომლებიც მზის მექანიზმის გარშემო ბრუნავს. პლანეტის მატარებელზე დამონტაჟებული, ისინი ერწყმის როგორც მზის, ასევე რგოლისებრ მექანიზმს. პლანეტის მექანიზმები თანაბრად ანაწილებენ დატვირთვას, რაც სისტემას მაღალი ბრუნვის მომენტის მართვის შესაძლებლობას აძლევს.

3.პლანეტის გადამზიდავიეს კომპონენტი აკავებს პლანეტარული მექანიზმების ადგილს და უზრუნველყოფს მათ ბრუნვას მზის მექანიზმის გარშემო. პლანეტარული მატარებლის ფუნქციას ასრულებს შემავალი, გამომავალი ან სტაციონარული ელემენტის როლი, სისტემის კონფიგურაციიდან გამომდინარე.

4.რგოლის მექანიზმიეს არის დიდი გარე მექანიზმი, რომელიც გარს ერტყა პლანეტარულ მექანიზმებს. რგოლისებრი მექანიზმის შიდა კბილები ერწყმის პლანეტარულ მექანიზმებს. სხვა ელემენტების მსგავსად, რგოლისებრ მექანიზმს შეუძლია შეასრულოს შეყვანის, გამოყვანის ფუნქცია ან დარჩეს უძრავად.

ამ ოთხი ელემენტის ურთიერთქმედება უზრუნველყოფს მოქნილობას, რათა მიღწეულ იქნას სხვადასხვა სიჩქარის თანაფარდობა და მიმართულების ცვლილებები კომპაქტურ სტრუქტურაში.

როგორ გამოვთვალოთ გადაცემათა კოეფიციენტი ეპიციკლურ გადაცემათა ნაკრებში?

გადაცემათა კოეფიციენტიეპიციკლური გადაცემათა ნაკრები დამოკიდებულია იმაზე, თუ რომელი კომპონენტებია ფიქსირებული, შემავალი და გამომავალი. აქ მოცემულია ეტაპობრივი ინსტრუქცია გადაცემათა კოეფიციენტის გამოსათვლელად:

1. სისტემის კონფიგურაციის გაგება:

დაადგინეთ, რომელი ელემენტია (მზე, პლანეტა-მატარებელი თუ რგოლი) სტაციონარული.

განსაზღვრეთ შეყვანის და გამოყვანის კომპონენტები.

2. გამოიყენეთ გადაცემათა კოეფიციენტის ფუნდამენტური განტოლება: ეპიციკლური გადაცემათა კოეფიციენტის გამოთვლა შესაძლებელია შემდეგი გამოყენებით:

GR = 1 + (R / S)

სად:

GR = გადაცემათა კოეფიციენტი

R = რგოლისებრი მექანიზმის კბილების რაოდენობა

S = მზის მექანიზმზე კბილების რაოდენობა

ეს განტოლება გამოიყენება მაშინ, როდესაც გამომავალი სიგნალი პლანეტის მატარებელია და ან მზე, ან რგოლისებრი მექანიზმი უძრავია.

3. სხვა კონფიგურაციებისთვის კორექტირება:

• თუ მზის მექანიზმი სტაციონარულია, სისტემის გამომავალი სიჩქარეზე გავლენას ახდენს რგოლისებრი მექანიზმისა და პლანეტის მატარებლის თანაფარდობა.
• თუ რგოლისებრი მექანიზმი სტაციონარულია, გამომავალი სიჩქარე განისაზღვრება მზის მექანიზმსა და პლანეტის მატარებელს შორის თანაფარდობით.

4. გამომავალი და შემავალი სიგნალების გადაცემათა კოეფიციენტის შებრუნება: სიჩქარის შემცირების გამოთვლისას (შემავალი სიგნალი გამომავალზე მაღალია), კოეფიციენტი მარტივია. სიჩქარის გასამრავლებლად (გამომავალი სიგნალი შემავალზე მაღალია), გამოთვლილი კოეფიციენტის ინვერტაცია.

მაგალითის გაანგარიშება:

დავუშვათ, გადაცემათა კომპლექტს აქვს:

რგოლისებრი მექანიზმი (R): 72 კბილი

მზის გადაცემათა კოლოფი (S): 24 კბილი

თუ პლანეტის გადამზიდავი არის გამომავალი და მზის გადაცემათა კოლოფი სტაციონარულია, გადაცემათა კოეფიციენტია:

GR = 1 + (72 / 24) GR = 1 + 3 = 4

ეს ნიშნავს, რომ გამომავალი სიჩქარე 4-ჯერ უფრო ნელი იქნება, ვიდრე შემავალი სიჩქარე, რაც უზრუნველყოფს 4:1 შემცირების თანაფარდობას.

ამ პრინციპების გააზრება ინჟინრებს საშუალებას აძლევს შექმნან ეფექტური და მრავალმხრივი სისტემები, რომლებიც მორგებულია კონკრეტულ აპლიკაციებზე.